鉛直面での円運動（糸、棒、壁）その３

この記事は「鉛直面での円運動（糸、棒、壁）その１、その２」を読んだことを前提に書かれています。

［有名題３］

長さ $r$ の糸に質量 $m$ の $P$ をつけ、最下点で初速 $v_0$ を与えて回すとき、 $P$ が１回転するための $v_0$ の条件を以下のように求めてみよう。

（１）半径方向のつり合いの式を求めよ。

（２）エネルギー保存の式を求めよ。

（３）（１）と（２）を連立させて、 $T$ を $\theta$ の式で表せ。

（４） $\theta=2\pi$ であっても $T \textgreater 0$ となるような $v_0$ の条件を求めよ。

（５） $P$ が１回転する条件を求めよ。

＝＝

さっそく解いてみましょう。

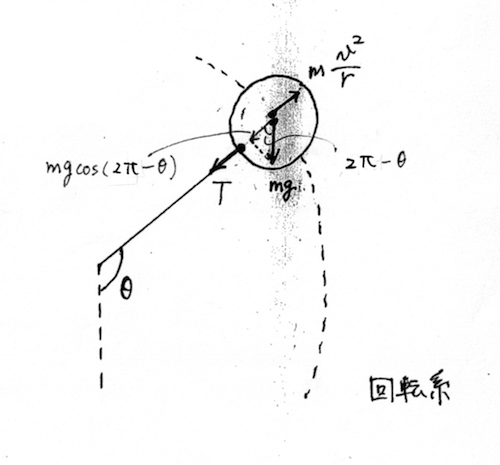
（１）半径方向のつり合いの式を求めよ。

回転系を使うと、図より半径方向のつり合いの式は

$T+ mg\cos(2\pi-\theta) - m\frac{v^2}{r}=0$

となります。ここで $2\pi-\theta$ は、「平行線の同側内角の和が $2\pi$ になること」から出しています。変形して

$T - mg\cos \theta -m\frac{v^2}{r}=0$ 　　　　　← $\cos(2\pi-\theta)=-\cos \theta$ ですからね

$T= mg\cos\theta + m\frac{v^2}{r}$

（２）エネルギー保存の式を求めよ。

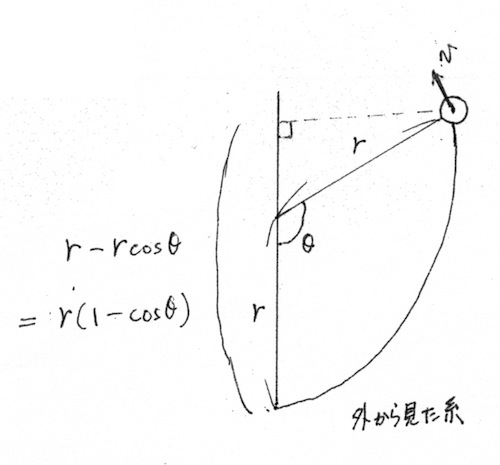
位置エネルギーを書き表さないといけないですよね。高低差を調べるために、一度外から見た系で図をスケッチしましょう。

$\frac{1}{2}mv^2 =\frac{1}{2}mv_0^2 -mgr(1-\cos \theta)$

これがエネルギー保存の式となります。図さえ書いてしまえば…というところでしょうか。なお、 $\theta$ が $\frac{\pi}{2}$ を超えているので、図と符号の一致に注意してください。

（３）（１）と（２）を連立させて、 $T$ を $\theta$ の式で表せ。

$T$ が $\theta$ によってどう変化するか調べてみましょう。（２）の結果を変形して

$\frac{mv^2}{r}=\frac{mv_0^2}{r}-2mg(1-\cos \theta)$

（１）の結果に代入して

$T=mg\cos \theta+\frac{mv_0^2}{r}-2mg(1-\cos \theta)$

$\raisebox{.2ex}{.}\raisebox{1.2ex}{.}\raisebox{.2ex}{.}$ $T=\frac{mv_0^2}{r}+mg(3\cos \theta -2)$

これで $T$ と $\theta$ の関係がわかりました。 $T\textless 0$ になると、糸がたるんでしまうのでしたね。

（４） $\theta=\pi$ であっても $T \textgreater 0$ となるような $v_0$ の条件を求めよ。

不等式 $T\textgreater 0$ を $\theta=\pi$ のもとで解きます。 $\cos\pi=-1$ ですから（３）の結果に代入して

$(T=)\frac{mv_0^2}{r}+mg\left\{3 \cdot(-1)-2\right\}\textgreater 0$

$\frac{mv_0^2}{r}-5mg\textgreater 0$

$v_0^2-5gr\textgreater 0$

$v_0\textgreater\sqrt{5gr}$

このような $v_0$ であれば、糸がたるまないことになります。以上（１）〜（４）までの結果と前投稿（有名題２）の結果より、「棒ではなく糸の場合の $P$ が１回転する条件」は

とわかりました。したがって求める条件は $v_0\textgreater\sqrt{5gr}$ となります。棒のときよりも、 $v_0$ が速くないといけない、より厳しい条件が課せられていることになります。

この話題は以上です。いかがだったでしょうか？直感と少し違う感じもしたのではないでしょうか！？

ではまた。

広島あおば物理塾