こんばん(にち)は、大魚です。
今日から数回にわたって、この時期につまずきやすい、不等速円運動の問題を取り上げてみましょう。
[有名題]
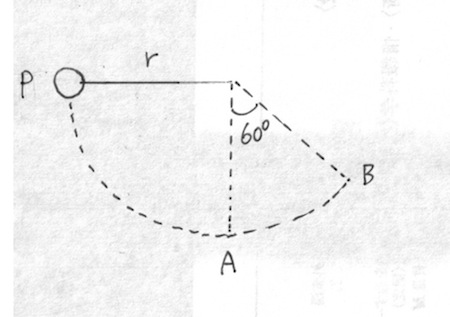
長さの糸に質量
のおもり
をつけ、水平にして放し、円運動させる。
(1)最下点Aでの糸の張力はいくらか。
(2)点Bでの張力はいくらか。
==
この問題では2通りの座標系を使って解くことが出来ます。1つは外から見た系、もう1つはおもりを固定した系(ここでは回転系と呼んでみます)です。どちらでもよいですが、回転系を使って解くと「慣性力が出現するかわりに、おもりが動いていることを頭の中から忘れることが出来る」ので、私はそちらの方が好きです。なお、慣性力
は暗記事項です。ではさっそく。
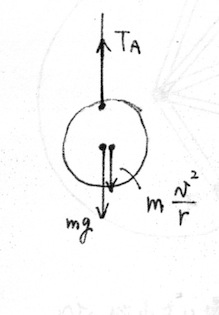
回転系から見るとおもりは動いていませんから、つり合いの式を立てることが出来ます。半径方向のつり合いの式は、図より
…(a)
エネルギー保存則は
…(b)
(b)より
(a)に代入して
つまり
これが答えとなります。
(2)回転系にて
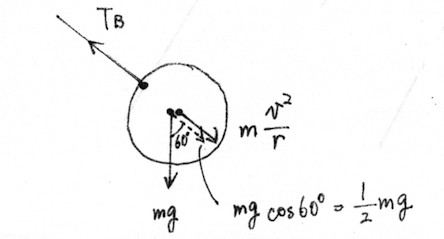
やはり回転系から見るとおもりは動いていませんから、つり合いの式を立てることが出来ます。半径方向のつり合いの式は、図より
…(c)
エネルギー保存則は
…(d)
(d)右辺の は、点Pと点Bの高度差になります。(d)より
これを(c)に代入して
つまり
これが答えとなります。
本日はここまでです。
次回は、この糸が棒に変わったり、あるいは糸でも棒でもなく小球が壁を這っていたりするときに、このパターンの問題がどうなるのかを取り上げたいと思います。